The unbearable effectiveness of ensembling
Want to make your neural networks uncertainty-aware? Let me teach you the ultimate technique: just train several model copies with different random seeds and average their predictions. Yes, it is this simple.
This approach is called deep ensemble, and it is a deceptively simple and surprisingly effective approach for uncertainty-aware learning. In fact, Ovadia et al. show that deep ensemble consistently beats all other non-ensemble methods, be it stochastic variational inference, Laplace approximation, MC dropout, or post-hoc calibration. It was a sad day for many BDL researchers.
Still wishing to contribute to the field, I followed the wise proverb “If you can’t beat them, join them”, and decided to have a closer look at the ensemble approach. This leads to our NeurIPS 2022 paper “Deep Combinatorial Aggregation” (DCA). And this post is a long-overdue introduction to our work.
Instead of simply repeating the results from the paper, I would like to share some “behind-the-scenes” stories on how this work is conceptualized and gradually developed. Maybe my personal experience can be of interest to fellow PhD students and researchers.
Starting point: rethinking ensemble
I have realized that there are only two ways to do research: you either generalize a too-simple approach, or simplify a too-complex one.
Seeing the simplicity of the deep ensemble approach, the first approach seems to be the way to go.
The initial idea
This work started with the following initial idea:
What if the ensemble is not at the model level?
For instance, what would happen if we have ensembles of layers? How would we train them? How should we perform inference with them?
These questions led me to test what is called layerwise DCA: Create multiple copies of each weight layer in the NN model, then select random combinations of these layers to produce model samples for every training and inference step.
One cool feature of this idea is that it generates an exponentially growing number of model samples with increasing model depth. For example, even for a simple model like VGG13, the same storage space for 5 deep ensemble model samples can host 5^13 = 1,220,703,125 layerwise DCA model samples! We would thus expect more diverse predictions from layerwise DCA.

Exponential model samples are bound to yield some impressive results, right? I was really excited about this idea and implemented some proof-of-concept experiments.
But … it doesn’t work!
Sadly, it turns out that layerwise DCA yields worse results compared to deep ensemble, even with its exponential model samples.
I was so sure that layerwise DCA could yield something interesting that this negative result hit me really hard: how could this awesome idea not work at all ?! ![]()
What to do with negative results
After sleeping away the frustration at the negative results, I still felt that there could be more to this idea and decided to dig a bit deeper.
Analysis and ablation studies
To begin with, I realized that I have only been testing with combinations of layer copies. What if we perform DCA with copies of multi-layer structures like residual block, or at the even coarser modelwise level? What if DCA happens instead at the finer intra-layer channelwise level?
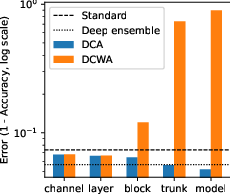
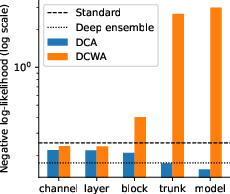
It seems that an ablation study is in order and it should hopefully provide more insights. I tested DCA at various granularities, ranging from the finest-grain intra-layer channel level DCA up to the coarsest-grain modelwise DCA.
The results show a clear trend: the coarser the granularity of DCA, the better the test results. This is also visible in the figure below. This means that modelwise DCA actually produces the best results!
Changing the perspective
Does it mean that finer-grain DCAs are simply useless? If so, the whole DCA idea wouldn’t be very interesting, since Modelwise DCA is very similar to the vanilla deep ensemble method. Luckily, this is not the case if we go beyond the perspective of direct performance comparison.
One day, taking inspiration from stochastic weight averaging (SWA), I started to investigate if weight averaging would also make sense for DCA copies. This leads to the deep combinatorial weight averaging (DCWA) approach discussed in the paper.
The main takeaway is that DCWA yields results comparable to SWA, but DCWA is effective only with fine-grain (intra-)layerwise DCA (cf. the figure above). SWA has some quirks, such as the need to re-evaluate the BatchNorm statistics and additional post-training update steps. DCWA does not have these quirks and is thus an interesting alternative.

Find and solve the problem
While DCWA is an encouraging result, it is still important to understand why finer-grain DCAs have worse results and try to address it.
In fact, this can be expected from a probabilistic perspective: freely combining DCA copies from each part implies that they follow independent distributions, which is not true in practice since the weights in a network are clearly correlated. Finer-grain DCAs make more unrealistic approximations, which might explain their worse results.
Is it possible the improve the results? I realized that the gradient updates for DCA copies can be inconsistent, since they originate from backpropagating through different model samples. This might be a reason for the suboptimal results.
To reduce the inconsistency, I decided to add a term to encourage the predictions from different model samples to agree with each other. The results in the consistency enforcing loss (CEL) proposed in the paper.
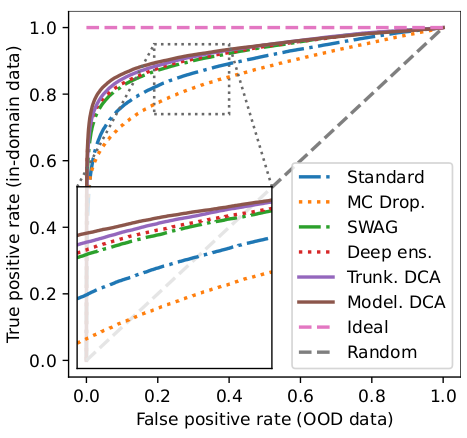
We found out that CEL trades off diversity for more consistency. Experiments show that it can improve the overall performance of DCWA as well as the uncertainty estimation of modelwise DCA.
What if nothing is working?
Open an English dictionary, what is typically the first verb on the word list? Yes, abandon ![]() .
.
Yep, often ideas just don’t work. Simply note down the results and move on to something new. You can always revisit when you come up with another relevant new idea.
Luckily the idea actually works this time, and it ends up making a contribution to the field! ![]()
Conclusion
I hope you have enjoyed this behind-the-scene story of our work. If you are interested in the details of our paper. Feel free to have a look!
Yuesong Shen, Daniel Cremers, “Deep Combinatorial Aggregation”, NeurIPS 2022
Source code on Github: https://github.com/tum-vision/dca
@inproceedings{shen2022dca,
author = {Shen, Yuesong and Cremers, Daniel},
booktitle = {Advances in Neural Information Processing Systems (NeurIPS)},
title = {Deep Combinatorial Aggregation},
year = {2022}
}
Until next time ![]()
